Binary
At its most general meaning, “binary” refers to any system composed of two elements. For example, a binary star system is a system in which there are two stars that orbit each other. Binary is also a numbering system that is comparable to our standard decimal system. The decimal system uses 10 digits; 0 through 9, and is referred to as a base-10 system. The binary system only has two digits, 0 and 1, so is referred to as a base-2 system.
Binary in Computing
Binary is essential to the computing industry. Computers at their lowest level perform all of their computations by manipulating the flow of electricity to indicate “on” and “off” states. These two states of electricity represent ones and zeroes to the computer, and these binary digits, or “bits,” can be strung together to represent numbers, characters, sound waves, or anything else that can be described digitally.
Because of the way the binary system works, every time you add a bit you double the capacity of the number. Picture each bit like a light switch; it can be set to either on or off. With one light switch, or bit, you only have two different states, so you can only have a 0 or a 1. If you had two switches, though, you have four possible outcomes.
- Both switches off
- Switch “A” on, switch “B” off
- Switch “A” off, switch “B” on
- Both switches on
Position matters in binary. If you count on your fingers, and you hold up any one of your fingers, you would interpret that as “one.” However, because a computer only has one “finger” at any given time, it has to count the position of the ones and zeroes in order to interpret them.
The size of the numbers the computer works with is equal to 2 to the power of the number of bits you have. However, keep in mind that the computer always starts counting at 0. So, with a 2 bit number, the computer can count up to 3; 2 times 2 is 4, but remember, the computer starts at 0.
If you have 4 bits, you can describe sixteen states; 0 through 15 (2 * 2 * 2 * 2 = 16). 5 bits gets you 32 states (2 * 2 * 2 * 2 * 2 = 32), and so on. The most common multiple of the bit is the byte, which is 8 bits of data. A byte allows the computer to count from 0 to 255, which equals 256 states.
Converting Numbers To and From Binary
To convert a number from a binary string composed of zeroes and ones to the decimal system we humans use on a day-to-day basis is a fairly simple procedure. The following diagram describes how you can convert any binary number into decimal. For this example, we’ll use the binary number “01100100.”
| 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | |||||||||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |||||||||
| 0 | + | 1 | + | 1 | + | 0 | + | 0 | + | 1 | + | 0 | + | 0 | = | 100 |
Starting on the right and moving left, each digit represents an increasing power of 2 to the power of the position. The first digit on the right represents 2 to the 0th power, or 1 (Any number to the 0th power is 1). Moving left, the next digit is 2 to the 1st power, or 2 (any digit to the first power is itself.) The next digit is 2 to the 2nd power, or 4.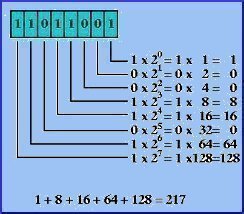
So, to convert a number from binary, you just add up the numbers of each position where you have a one. We have a 1 in the 4 position, so we add 4 to our number. We have a 1 in the 32 position, so we add 32. We also have a 1 in the 64 position, so we add 64. Then we just add those together: 64 + 32 + 4 = 100.
To convert from decimal to binary, we basically do the reverse. If we wanted to convert 113 to binary, we would go through each position and ask if that number can go into our number. Can 128 go into 113? No. Can 64? Yes, so put a 1 in the 64 position. Subtract 64 from 113 and we have 49 remaining. Can we subtract 32 from 49? Yes, so put another 1 in the 32 position. We have 17 remaining. Put a 1 in the 16 position and a 1 in the 1 position. So the binary representation of 113 is “01110001.”
| 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | |||||||||
| 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | |||||||||
| 0 | + | 1 | + | 1 | + | 1 | + | 0 | + | 0 | + | 0 | + | 1 | = | 113 |


Comments - No Responses to “Binary”
Sorry but comments are closed at this time.