A graph is an important non linear data structure. This data structure is used to represent relationship between pairs of elements, which may not, necessarily, be hierarchical in nature.

A graph is defined as: “Graph G is an ordered set (V, E), where V(G) represents the set of elements, called vertices, and E(G) represents the edges between these vertices.”

Graphs can be of either type,

  • Undirected Graph
  • Directed Graph

Figures below show sample graphs.

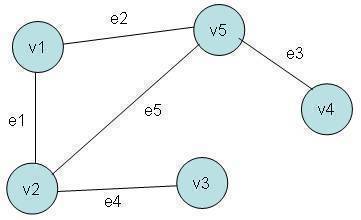
V(G) = { v1, v2, v3, v4, v5 } E(G) = { e1, e2, e3, e4, e5 }

Undirected Graph

Directed Graph

Graph Terminologies

  • Adjacent Vertices An edge e is represented by a pair of vertices denoted by [u, v]. The vertices u and v are called endpoints of edge e. These vertices are also called adjacent vertices or neighbors.
  • Degree of a Vertex The degree of vertex u, written as degree(u) or d(u), is the number of edges containing u. If d(u) = 0, this means that vertex u does not belong to any edge, then vertex u is called an isolated vertex.
  • Path A path P of length n from a vertex u to vertex v is defined as sequence of (n + 1) vertices, i.e., P = (v 1, v 2, v 3 …v n+1). The path is said to be closed if the endpoints or end-vertices of the path are same, i.e., v 1 = v n+1. The path is said to be simple if all the vertices in the sequence are distinct, with the exception that v 1 = v n+1. In latter case, it is known as closed simple path.
  • Cycle A cycle is closed simple path with length of 2 or more. Sometimes, a cycle of length k (i.e., k distinct vertices in the path) is known as k-cycle.
  • Connected Graph A graph is said to be connected if there exist a path between any two of its vertices, i.e., an isolated vertex does not exist. A connected graph without any cycles is called a tree. Thus we can say that tree is a special graph.
  • Complete Graph A graph G is said to be complete or fully connected if there exist a path from every vertex to every other vertex. A complete graph with n vertices will have (n (n-1))/2 edges.
  • Weighted Graph A graph is said to be a weighted graph if every edge in the graph is assigned some data or value. The weight is denoted by w(e). w(e) is non negative value that may be representing the cost of moving along that edge or distance between the vertices.

  • Multiple Edges Distinct edges e and e’ are called multiple edges if they connect the same end points, i.e., if e = [u, v] and e’ = [u, v].
  • Loop An edge is a loop if it has identical endpoints, i.e., if e = [u, u].

Directed Graph Terminologies

  • Directed Graph A directed graph G is a graph in which each edge is assigned a certain direction, i.e., each edge is ordered pair of (u, v) of vertices rather than an unordered pair [u, v]. Suppose Gis a directed graph with e = (u, v) as one of the edge, then, e begins at u and ends at v. u is the origin of e, and v is the destination of e. u is predecessor of v, and v is the successor of u.
  • Out-degree and In-degree of a Vertex The out-degree of vertex u, denoted by outdegree(u), is the number of edges originating at u. The in-degree of a vertex u, denoted by indegree(u), is the number of edges terminating at u.
  • Source and Sink A vertex u is called a source if it has an out-degree greater than zero, but zero in-degree. A vertex u is called a sink if it has an in-degree greater than zero, but zero out-degree.
  • Reach-ability Vertex v is said to be reachable from vertex u if there exists a path from vertex u to vertex v.
  • Strongly Connected A directed graph G is said to be strongly connected, if for each pair (u, v) vertices in G, if there exists a path from u to v, there must exist a path from v to u; otherwise the directed graph is unilaterally connected.
  • Parallel Edges Distinct edges e and e’ are called parallel edges if they connect the same source and terminal vertices, i.e., if e = (u, v) and e’ = (u, v).
  • Simple Directed Graph A directed graph G is said to be simple, if there are no parallel edges. A simple directed graph may have loops, but it can not have more than one loop at a given vertex.
  • Directed Acyclic Graph A directed acyclic graph G is a graph without any cycle(s).